Titanic - Quien Sobrevivió? - Parte 2
Esta publicación sigue a la Parte 1 que preparó los datos para que en esta Parte 2 se puedan analizar y un modelo de clasificación se pueda crear. El modelo se usará para predecir si un pasajero en el Titanic murió o sobrevivió.
2) Paquetes
Los siquientes paquetes se usan en esta publicación.
library(dplyr)
library(readr)
library(tidyr)
library(ggplot2)
library(knitr)
library(DT)
library(purrr)
library(corrplot)
library(randomForest)
library(caret)
library(rpart)
library(rpart.plot)3) Exploración de Los Datos
Ahora que los datos se han preparado en la Parte 1, el siguiente paso es llevar a cabo la exploración de los datos para comprender mejor sus características. Se utilizan los datos de entrenamiento.
setwd("~/Documents/Machine Learning/15. Hugo/academic-kickstart-master/content/es/post/Titanic2")
total <- read_csv("total2.csv")
total <- total[,-1]
ensayo <- read.csv("test.csv")
entrenar <- read.csv("train.csv")3.1) Pclass
El gráfico a la continuación muestra la supervivencia de pasajeros para cada uno de los tres clases sociales a bordo del Titanic. Rojo representa pasajeros que murieron, y azul los que sobrevivieron. La línea blanca es la tasa de supervivencia promedia para todos los pasajeros en los datos de entrenamiento - 38.38%.
Los pasajeros en primera clase tuvieron una tasa de supervivencia superior al promedio de 62.5%. Los pasajeros de segunda clase siguieron esta tendencia, aunque con una tasa de supervivencia más cercana al 50%. En comparación, los pasajeros de tercera clase tenían una tasa de supervivencia de solo el 25%.
ggplot() +
geom_bar(data = total %>% filter(group == 'train'), aes(Pclass, fill = as.factor(Survived)), position = 'fill') +
geom_hline(yintercept = 0.3838, col = "white", lty=2, size=2) +
scale_fill_brewer(palette="Set1") +
ylab("Tasa de Supervivencia") +
xlab("Clase") +
ggtitle("Tasa de supervivencia por clase") +
labs(fill = "Sobrevivió") +
theme_minimal()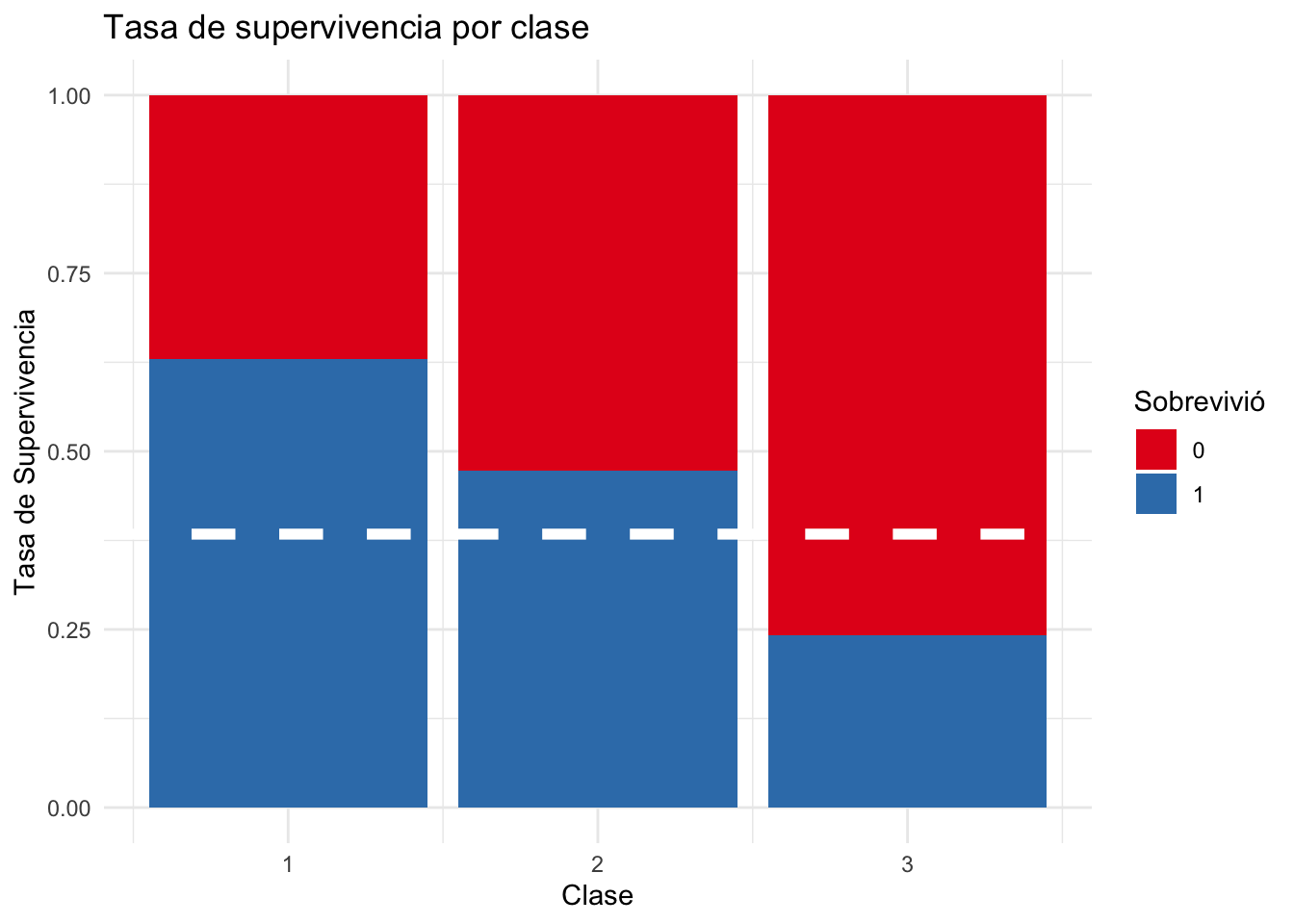
3.2) Título
El gráfico a continuación muestra como los pasajeros con el título ‘Mr’ tenían una tasa de supervivencia muy bajo. En comparación, un niño con el título ‘Master’ o una mujer con el título ‘Miss’ tenía una mejor probabilidad de supervivencia con tasas de supervivencia más cercanos al 70%.
ggplot() +
geom_bar(data = total %>% filter(group == 'train'), aes(Title, fill = as.factor(Survived)), position = 'fill') +
geom_hline(yintercept = 0.3838, col = "white", lty=2, size=2) +
scale_fill_brewer(palette="Set1") +
ylab("Tasa de Supervivencia") +
xlab("Título") +
ggtitle("Tasa de supervivencia por título") +
labs(fill = "Sobrevivió") +
theme_minimal()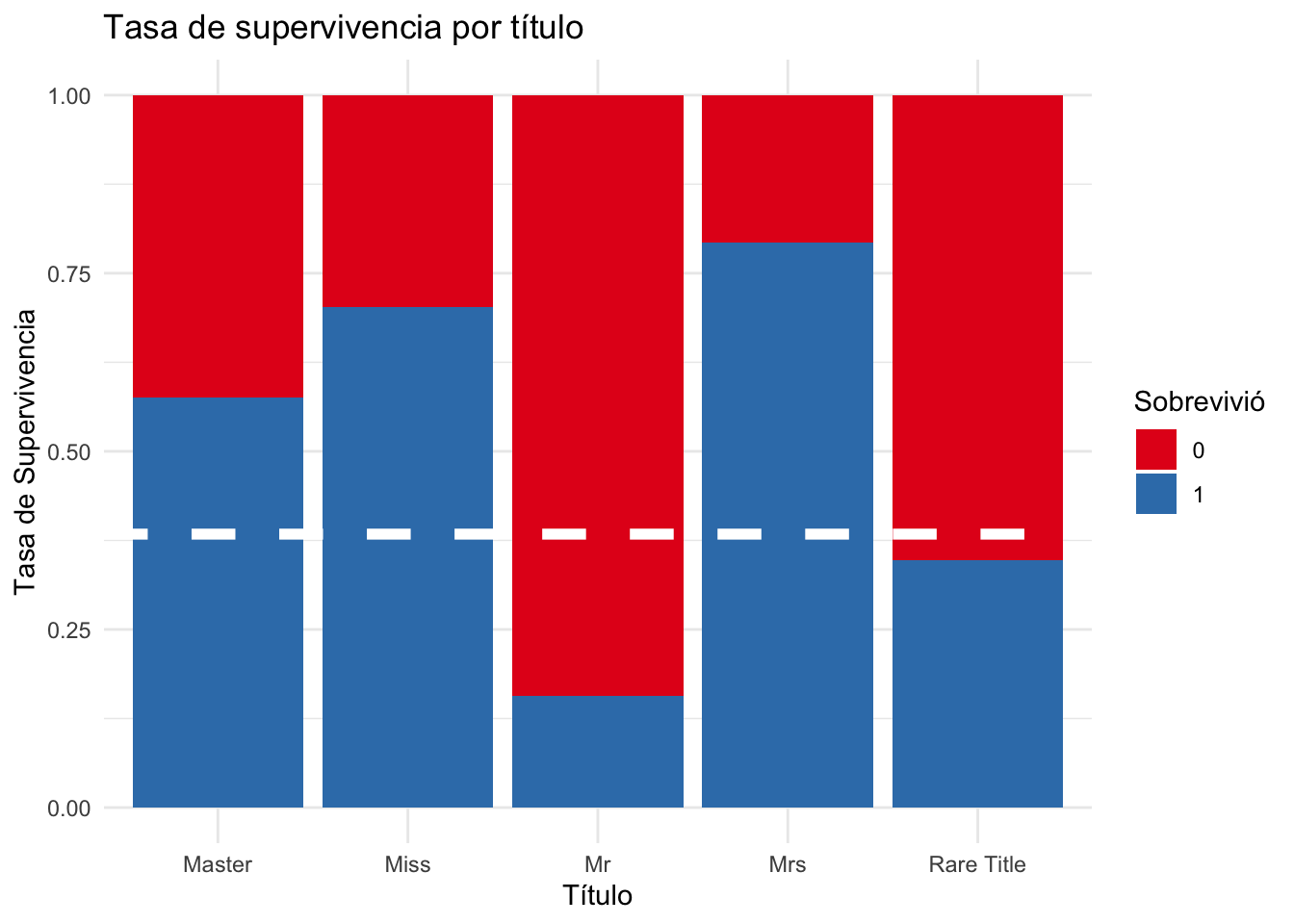
3.3) Puerto
Había tres puertos de embarque: Southampton, Reino Unido; Cherborg, Francia; y Queenstown, Irlanda. No hay tanta diferencia en la tasa de supervivencia entre los tres puertos, no obstante pasajeros que embarcaron en Cherborg tenían la tasa más alta.
ggplot(total %>% filter(group=="train"), aes(Embarked, fill=as.factor(Survived))) +
geom_bar(position = "fill") +
scale_fill_brewer(palette="Set1") +
ylab("Tasa de Supervivencia") +
geom_hline(yintercept=0.38, col="white", lty=2, size=2) +
ggtitle("Tasa de supervivencia por Puerto") +
xlab("Puerto") +
labs(fill = "Sobrevivió") +
theme_minimal()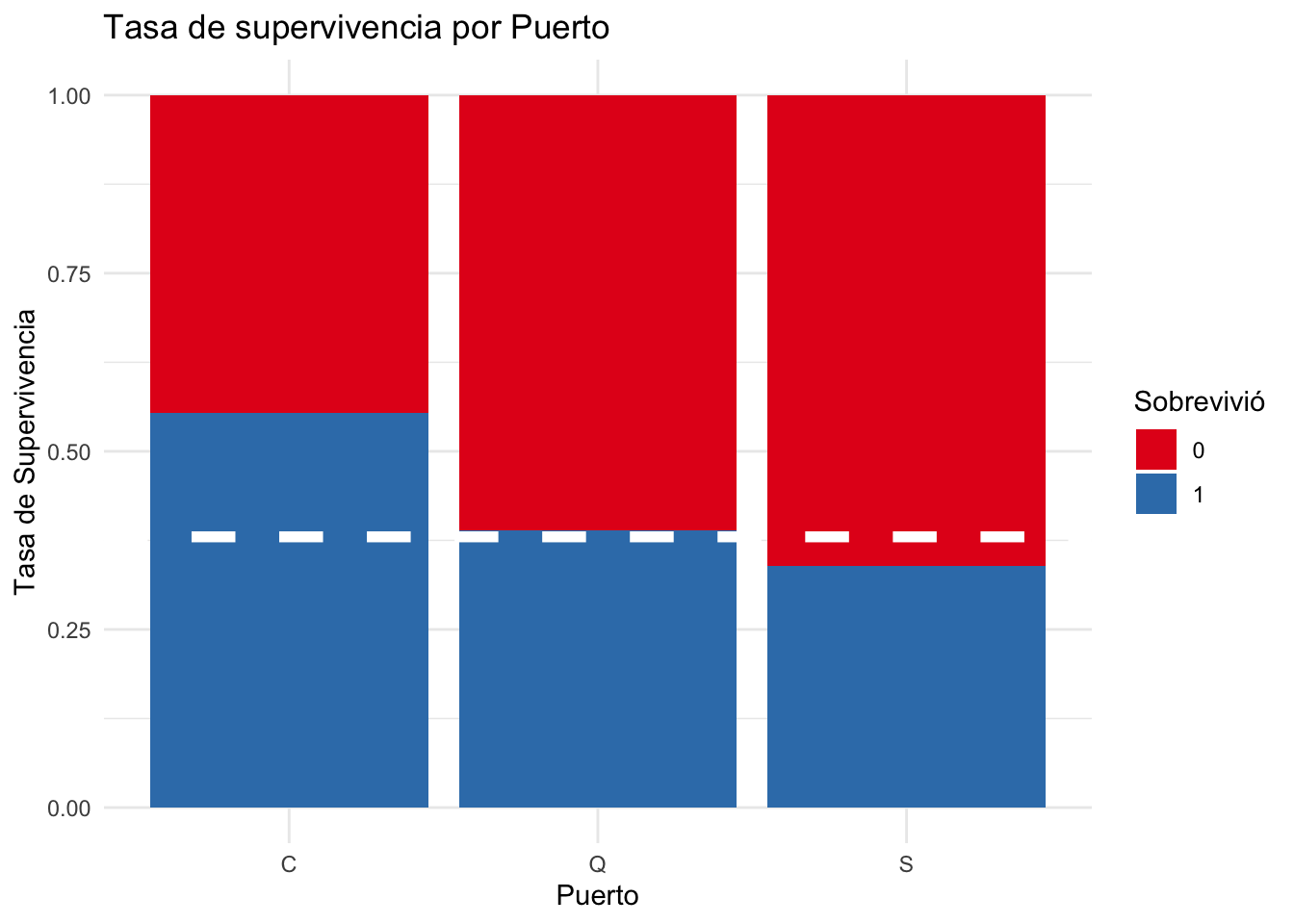
3.4) Tarifa y Clase
El siguiente gráfico muestra la relación entre supervivencia y tarifa. Sugiere que los pasajeros con los pasajes más caros eran los que tenían más probabilidades de sobrevivir. Por ejemplo, hay una mayor concentración de pasajes que costaban más de £50 en pasajeros supervivientes.
ggplot(total %>% filter(group=="train"), aes(Fare, Survived)) +
geom_point() +
ylab("Tasa de Supervivencia") +
xlab("Tarifa") +
ggtitle("Supervivencia contra Tarifa") +
theme_minimal()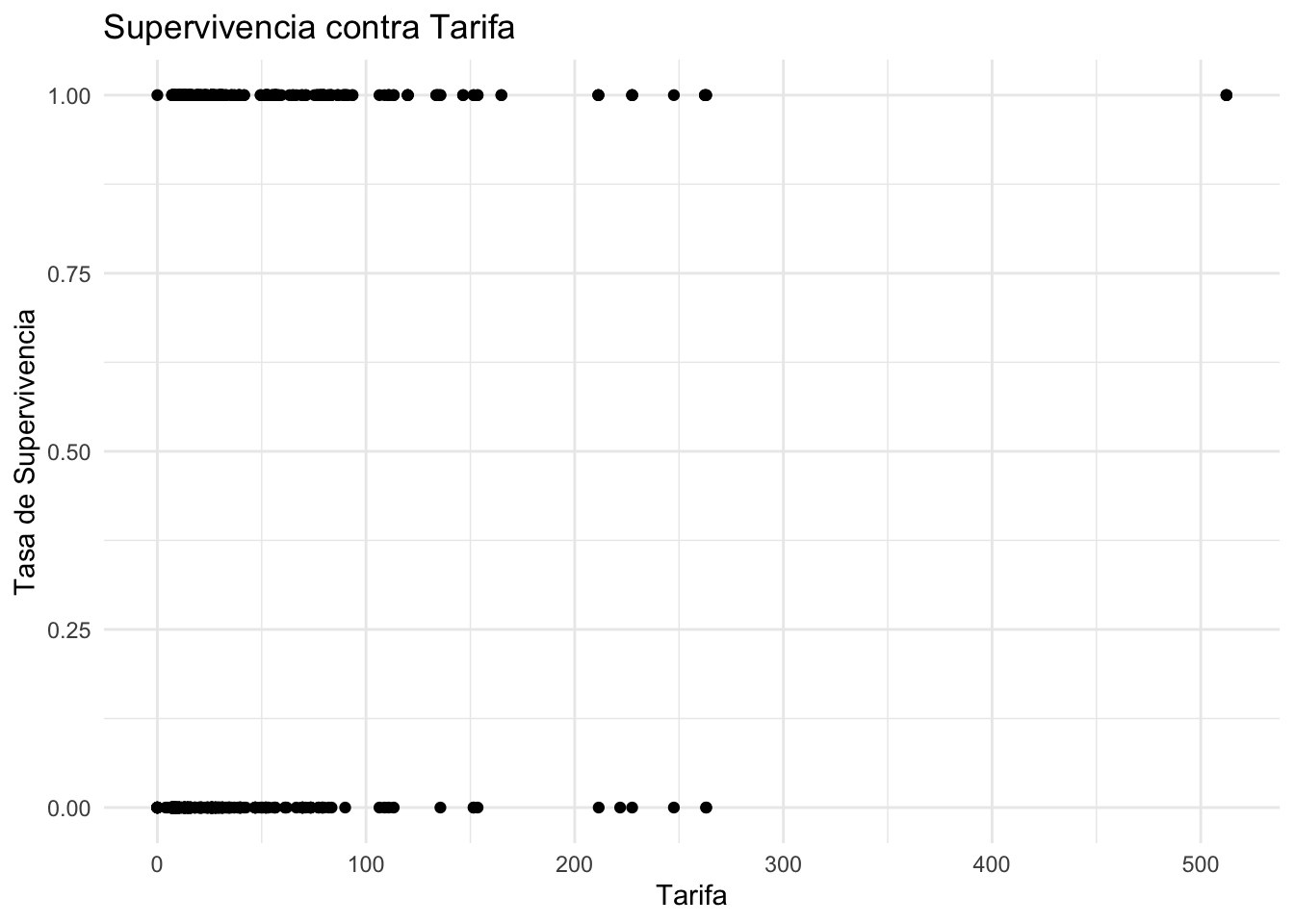
Además, se puede trazar la clase contra la tarifa para ver cómo se dividían las tarifas entre las clases. Este gráfico sugiere que existe una correlación entre tarifa y clase. Por lo tanto, a continuación se revisa esta correlacion ya que podría causar multicolinealidad.
ggplot(total %>% filter(group=="train"), aes(Pclass, Fare)) +
geom_point() +
ylab("Tarifa (£)") +
xlab("Clase") +
ggtitle("Clase contra Tarifa") +
theme_minimal()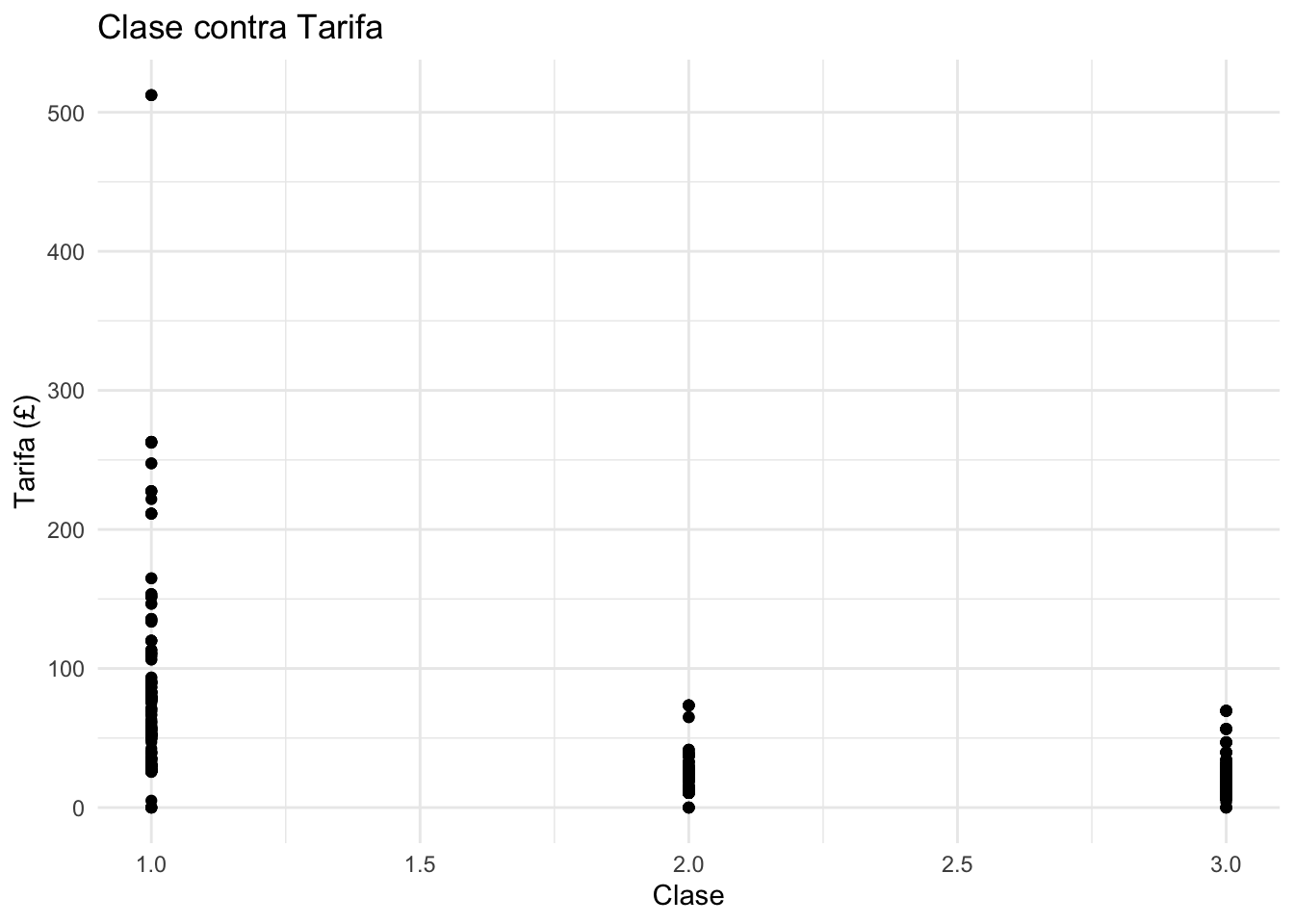
3.4.1) Sobre Correlación
Continuando con la sugerencia previa de una correlación entre clase y tarifa, se calcula la correlación entre estas dos variables. El siguiente gráfico muestra que existe una correlación negativa de 0,55. Esta alta correlación podría ser perjudicial para el modelo, ya que la clase y la tarifa son correlacionadas y tienen un impacto parecido en la variable dependiente. Este impacto parecido se llama multicolinealidad. Por lo tanto, la tarifa no se incluirá en el modelo.
tbl_corr <- total %>%
filter(group=="train") %>%
select(-PassengerId, -SibSp, -Parch) %>%
select_if(is.numeric) %>%
cor(use="complete.obs") %>%
corrplot.mixed(tl.cex=0.85)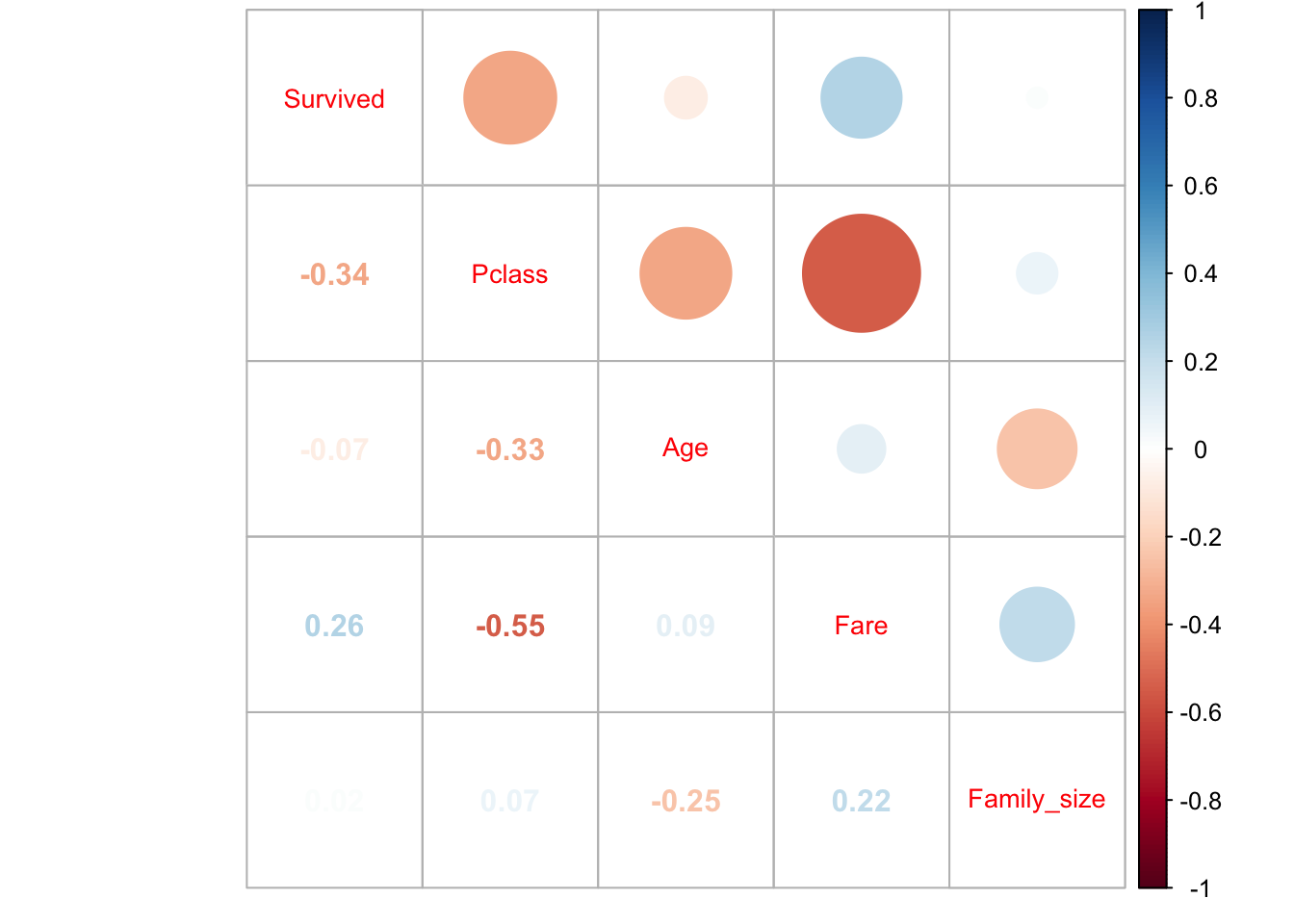
3.5) Sexo
Este gráfico muestra que las mujeres tenían una tasa de supervivencia más alta que los hombres. Casi el 75% de las mujeres sobrevivieron en comparación con aproximadamente el 23% de los hombres.
ggplot(total %>% filter(group=="train"), aes(Sex, fill=as.factor(Survived))) +
geom_bar(position = "fill") +
scale_fill_brewer(palette="Set1") +
ylab("Tasa de Supervivencia") +
geom_hline(yintercept=0.38, col="white", lty=2, size=2) +
ggtitle("Tasa de Supervivencia por Sexo") +
xlab("Sexo") +
labs(fill = "Sobrevivió") +
theme_minimal()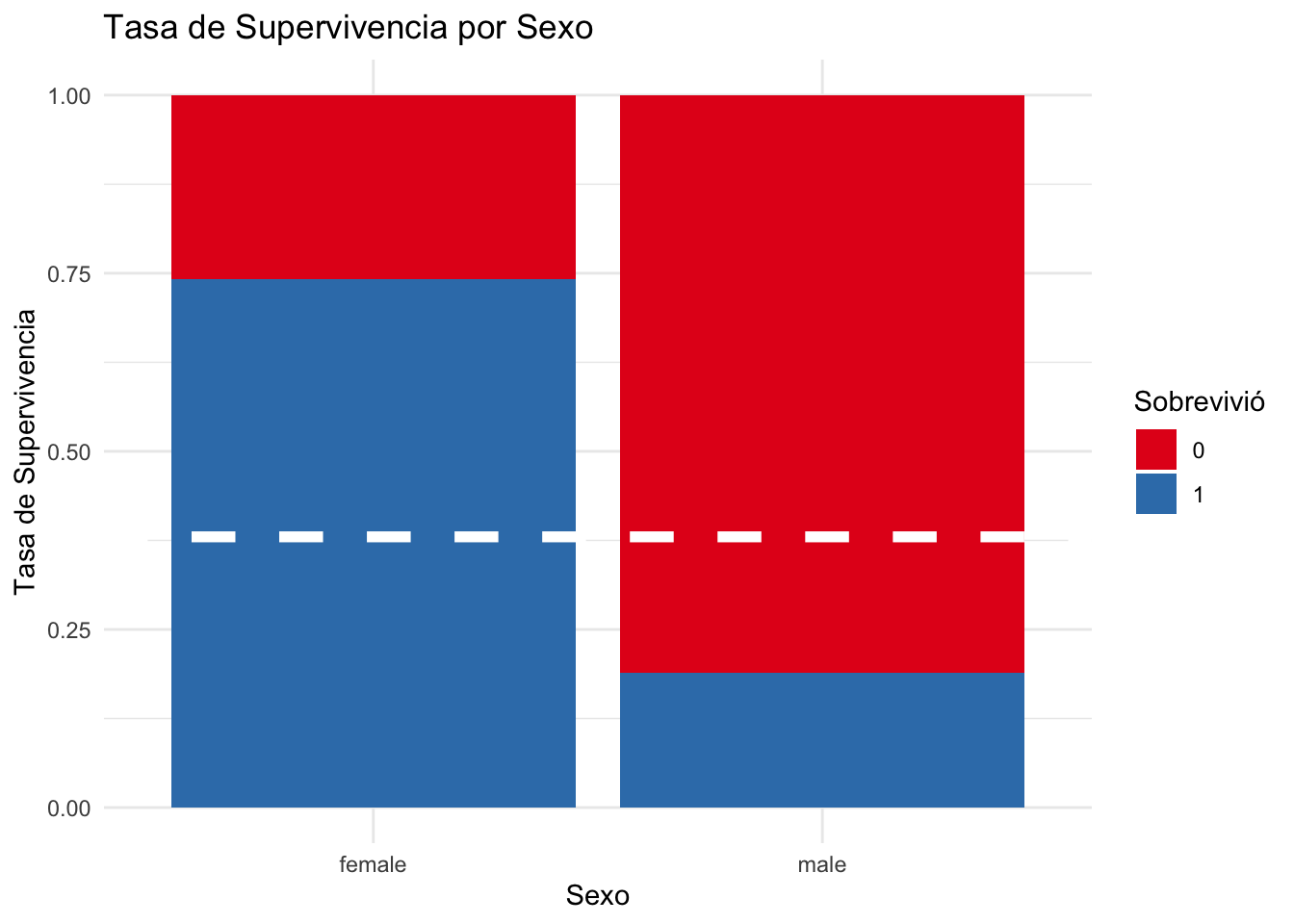
3.5.1) Sexo y Clase
El siguiente gráfico muestra cómo el sexo tuvo un gran impacto en la tasa de supervivencia. Ser una mujer de primera o segunda clase era casi una característica de supervivencia. Además, aproximadamente el 50% de las mujeres de la tercera clase sobrevivieron. En comparación con estas cifras, la tasa de supervivencia para los hombres, independientemente de la clase, nunca fue más alta que la tasa promedia para todos los pasajeros.
ggplot(total %>% filter(group=="train"), aes(Pclass, fill=as.factor(Survived))) +
facet_wrap(~Sex, scale = "free") +
geom_bar(position = "fill") +
scale_fill_brewer(palette="Set1") +
ylab("Tasa de Supervivencia") +
geom_hline(yintercept=0.38, col="white", lty=2, size=2) +
ggtitle("Tasa de Supervivencia por Sexo y Clase") +
xlab("Clase") +
labs(fill = "Sobrevivió") +
theme_minimal()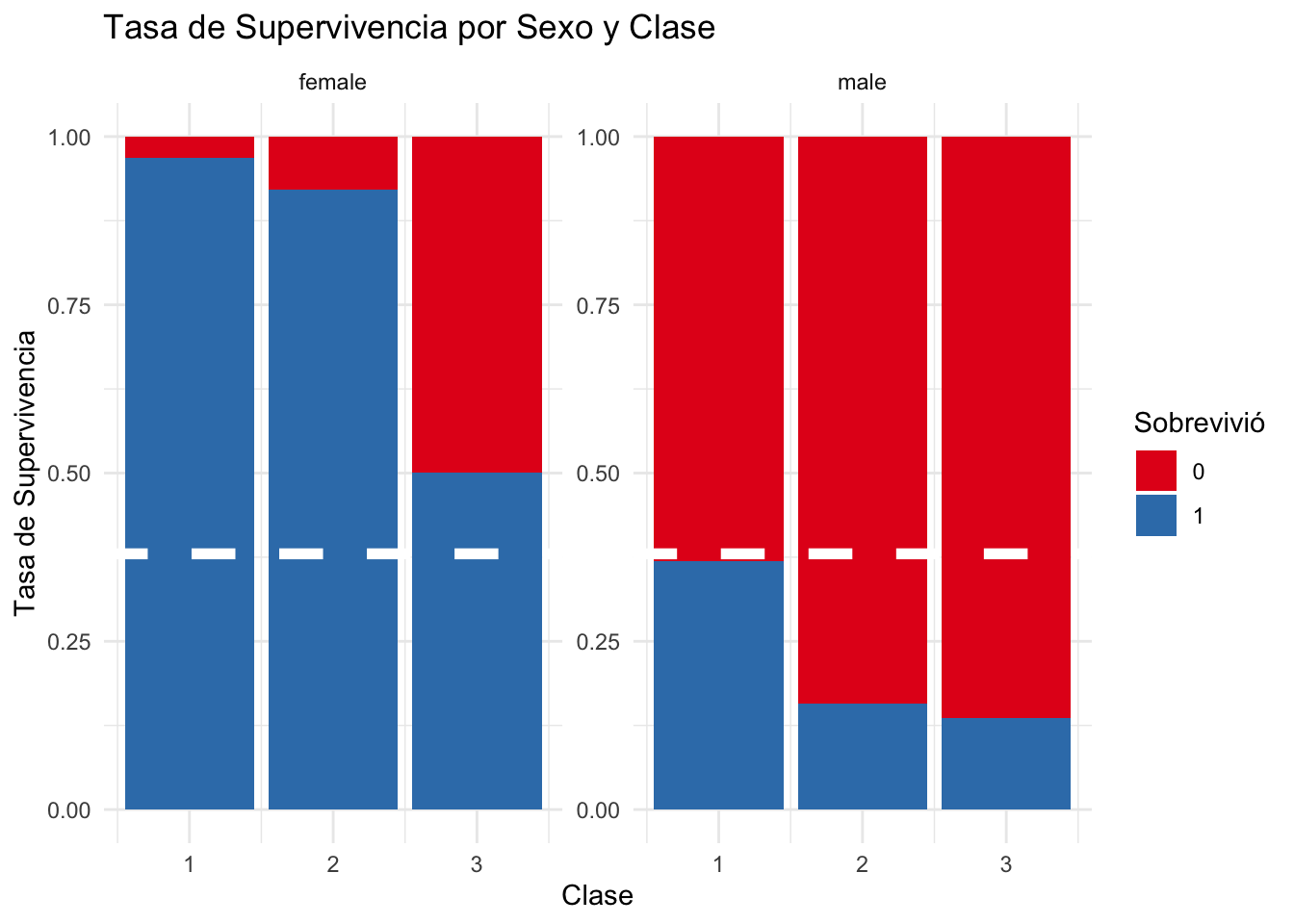
3.5.2) Cherborg, Sexo y Clase
El grafico a la continuacion divide las variables de Port, Sex, y Class para ver como estas variables impactaron supervivencia. Algunos patrones se identifican.
Primero, casi todas las mujeres de la primera y segunda clase sobrevivieron, independiente del puerto donde comenzaron su viaje. Mujeres de la primera clase no tuvieron tanto suerte con tasas de supervivencia mas bajas en cada uno de los puertos de embarque. También se nota que las mujeres de tercera clase de Southampton tenían una tasa de supervivencia particularmente más baja que las otras mujeres.
En relación con los pasajeros masculinos, hubo mayores tasas de supervivencia para aquellos que habían abordado el barco en Southampton y Cherborg. Además, Cherborg tenía la tasa de supervivencia masculina más alta para cada una de las tres clases. Finalmente, casi todos los hombres de Queenstown murieron.
Lamentablemente, como se explica en parte 1, hay muchos valores faltantes para los datos de cabinas ya que hubiera sido interesante analizar como pasajeros de diferentes puertos tenían cabinas en diferentes ubicaciones en el Titanic, con estas ubicaciones impactando su probabilidad de supervivencia.
ggplot(total %>% filter(group=="train"), aes(Embarked, fill = as.factor(Survived))) +
facet_wrap(~Sex ~Pclass, scale = "free") +
geom_bar(position = "fill") +
scale_fill_brewer(palette="Set1") +
ylab("Tasa de Supervivenica") +
ggtitle("Tasa de Supervivenica por Puerto") +
labs(fill = "Sobrevivió") +
xlab("Puerto") +
geom_hline(yintercept=0.38, col="white", lty=2, size=2) +
theme_minimal()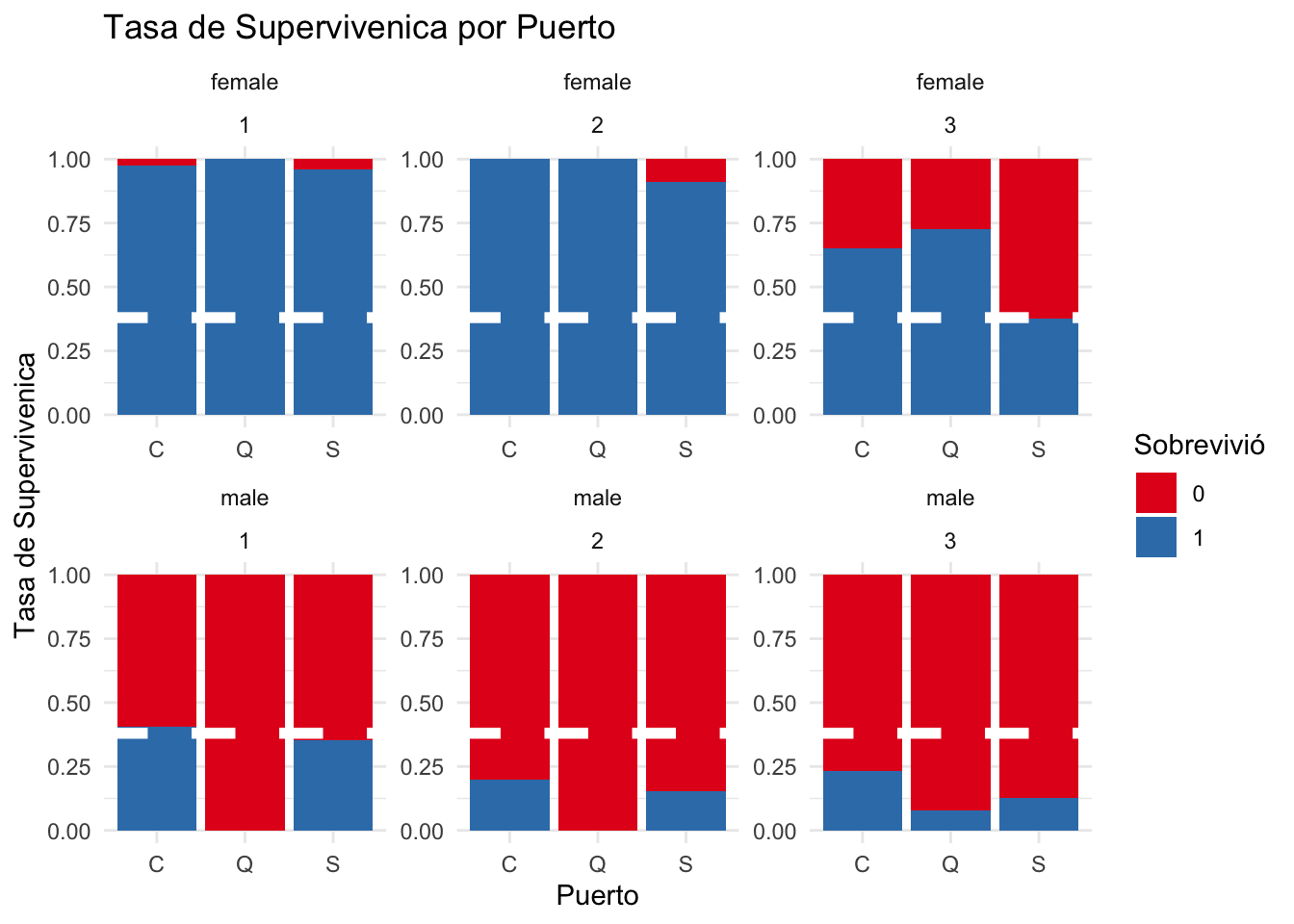
3.6) Tamaño de Familia
En el gráfico a continuación se observa que las familias de dos, tres o cuatro personas en el Titanic tenían una mayor tasa de supervivencia.
ggplot(total %>% filter(group=="train"), aes(Family_size, fill=as.factor(Survived))) +
geom_bar(position = "fill") +
scale_fill_brewer(palette="Set1") +
ylab("Survival Rate") +
geom_hline(yintercept=0.38, col="white", lty=2, size=2) +
ggtitle("Tasa de Supervivencia por Tamaño de Familia") +
labs(fill = "Sobrevivió") +
xlab("Tamaño de Familia") +
theme_minimal()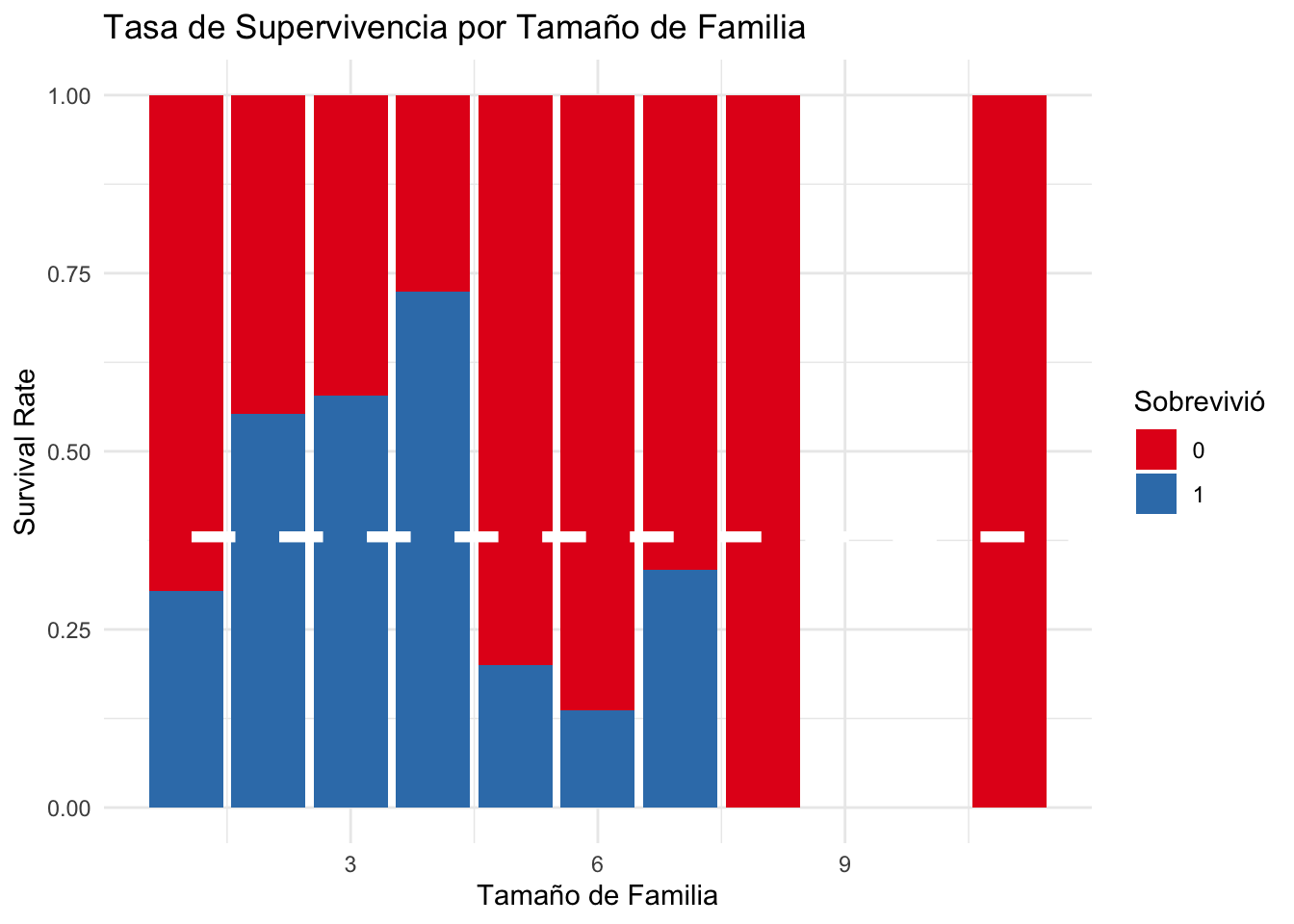
4) Creando Los Modelos
4.1) Preparación de Los Datos
Primero, se deben elegir las variables que se utilizarán en el modelo. Como se explicó anteriormente, no se utilizarán Fare ni Cabin. Las observaciones de entrenamiento y de ensayo se separan, y las observaciones de entrenamiento luego se dividen en dos grupos separados:
entrenar_val = 80% de las observaciones de entrenamiento
entrenar_ensayar_val = 20% de las observaciones de entrenamiento
El grupo entrenar_val se utiliza para entrenar el modelo. Luego, el modelo se ensaya primero con el grupo entrenar_ensayar_val. Los resultados de esta prueba se utilizan para ajustar el modelo de modo que se puedan utilizar los mejores ajustes.
Finalmente, el modelo se prueba utilizando los datos de prueba reales, los que tienen la variable dependiente oculta.
feauter1 <-total[1:891, c("Pclass", "Title","Sex","Embarked","Family_size","Age Group", "Survived")]
feauter1$Survived <- as.factor(feauter1$Survived)
set.seed(500)
ind <- createDataPartition(feauter1$Survived,times=1,p=0.8,list=FALSE)
entrenar_val <- feauter1[as.vector(ind),]
entrenar_ensayar_val <- feauter1[-ind,]4.2) La Distribución de La Variable Dependiente
La distribución de los pasajeros que sobrevivieron o murieron en los grupos entrenar_val y entrenar_ensayar_val se analiza para garantizar que haya una distribución equitativa de los resultados entre ambos grupos. La distribución de sobrevivientes y muertes entre los grupos es igual con una proporción de 6 muertes por 4 sobrevivientes.
round(prop.table(table(entrenar$Survived)*100),digits = 1)##
## 0 1
## 0.6 0.4round(prop.table(table(entrenar_val$Survived)*100),digits = 1)##
## 0 1
## 0.6 0.4round(prop.table(table(entrenar_ensayar_val$Survived)*100),digits = 1)##
## 0 1
## 0.6 0.44.3) Modelo de Árbol de Decisión
En esta seccion un modelo de árbol de decisión se crea con el grupo de entrenar_val. Luego se usan los datos del grupo de entrenar_ensayar_val para ensayar el model y hacer ajustes.
Habiendo creado el modelo la matriz de confusión se puede usar para ver su precisión. Tiene una precisión de 0.8389 y una kappa de 0.642. Ahora validación cruzada se usa para verificar el modelo.
set.seed(1234)
Model_DT <- rpart(Survived~.,data=entrenar_val,method="class")
rpart.plot(Model_DT,extra = 3,fallen.leaves = T)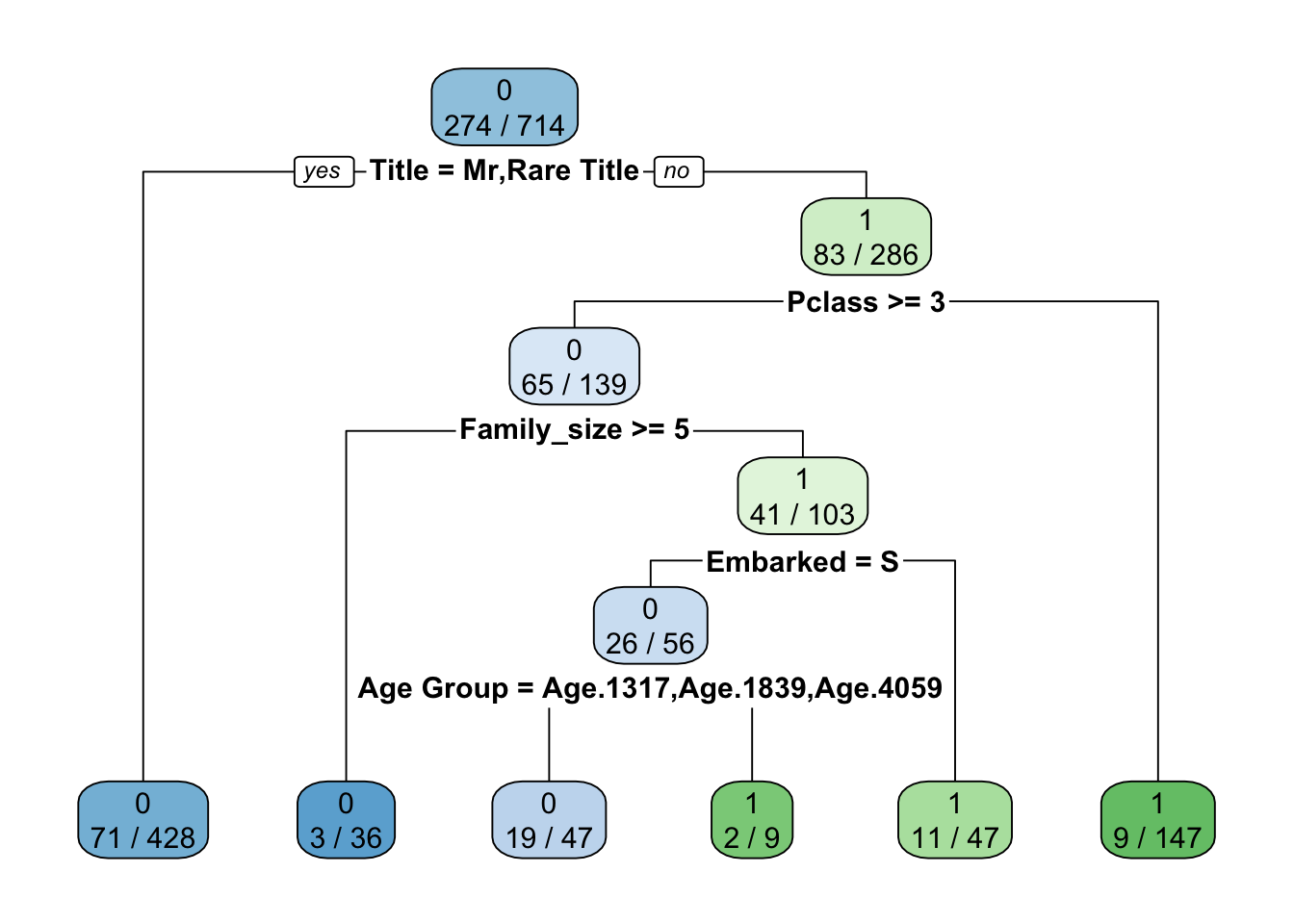
PRE_TDT=predict(Model_DT,data=entrenar_val,type="class")
confusionMatrix(PRE_TDT,entrenar_val$Survived)## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 418 93
## 1 22 181
##
## Accuracy : 0.8389
## 95% CI : (0.8099, 0.8652)
## No Information Rate : 0.6162
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.642
##
## Mcnemar's Test P-Value : 6.686e-11
##
## Sensitivity : 0.9500
## Specificity : 0.6606
## Pos Pred Value : 0.8180
## Neg Pred Value : 0.8916
## Prevalence : 0.6162
## Detection Rate : 0.5854
## Detection Prevalence : 0.7157
## Balanced Accuracy : 0.8053
##
## 'Positive' Class : 0
## 4.4) Validación Cruzada
La validación cruzada se usa diez veces para garantizar que se utilicen suficientes datos para crear el modelo y que se representen el rango completo de los datos completos. Con este método, el grupo entrenar_val se divide en diez partes. Cada parte se usa como grupo de prueba una vez y las otras nueve partes se usan como datos de entrenamiento. De esta manera, es menos probable que ocurra un sobreajuste.
set.seed(1234)
cv.10 <- createMultiFolds(entrenar_val$Survived, k = 10, times = 10)
# Control
ctrl <- trainControl(method = "repeatedcv", number = 10, repeats = 10,
index = cv.10)
entrenar_val <- as.data.frame(entrenar_val)
##Train the data
Model_CDT <- train(x = entrenar_val[,-7], y = entrenar_val[,7], method = "rpart", tuneLength = 30,
trControl = ctrl)
rpart.plot(Model_CDT$finalModel, type=4, clip.right.labs=FALSE, branch=.7)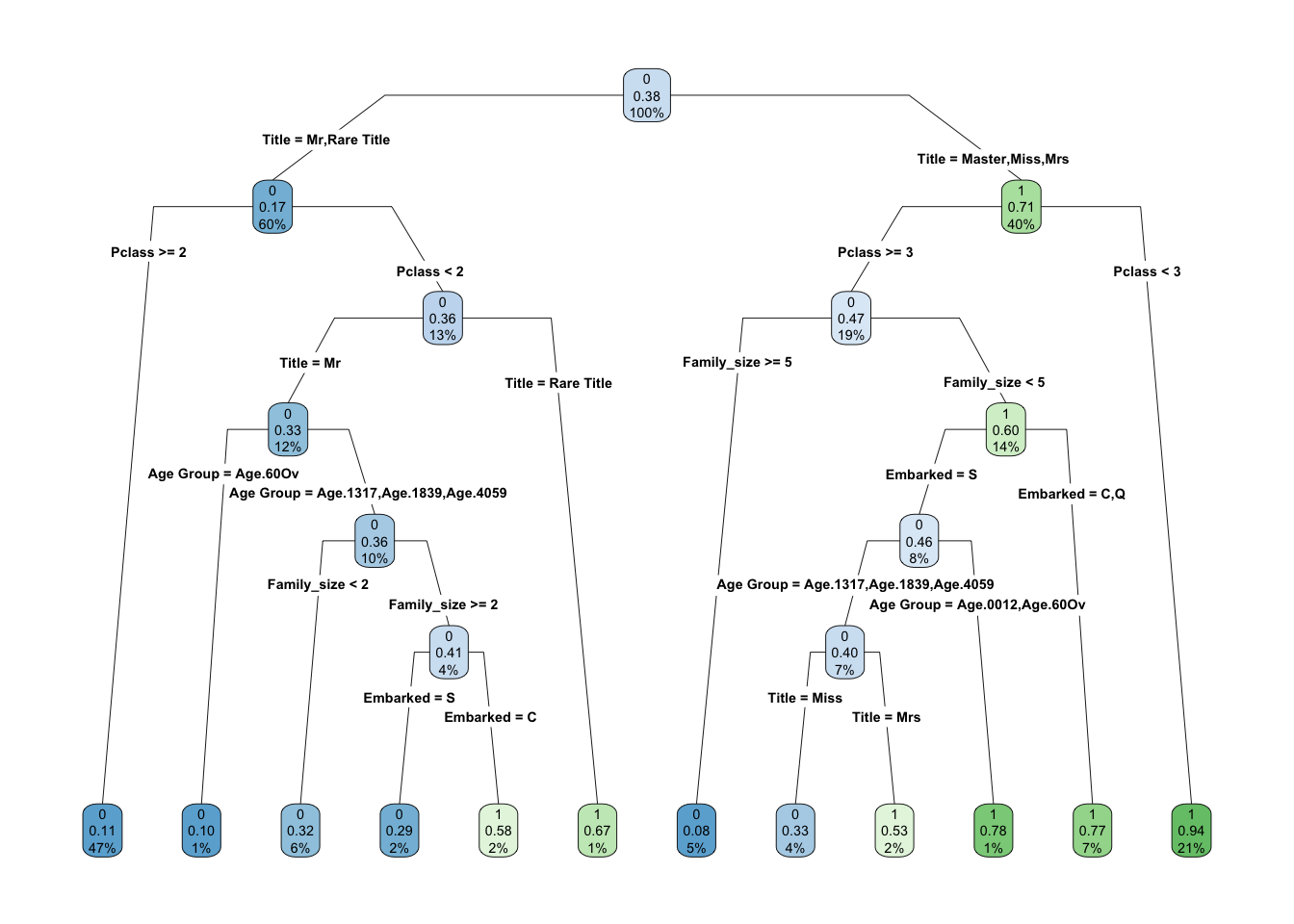
4.4.1) Validación Cruzada Predicciónes
La matriz de confusión de abajo expone que el modelo con validación cruzada tiene una precisión de 0.8079. Esta cifra es menos que el primero modelo que no utilizaba validación cruzada (0.8389). Por lo tanto, sugiere que sobreajuste pasaba con el primer modelo.
set.seed(1234)
PRE_VDTS=predict(Model_CDT$finalModel,newdata=entrenar_ensayar_val,type="class")
confusionMatrix(PRE_VDTS,entrenar_ensayar_val$Survived)## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 94 19
## 1 15 49
##
## Accuracy : 0.8079
## 95% CI : (0.7421, 0.8632)
## No Information Rate : 0.6158
## P-Value [Acc > NIR] : 2.854e-08
##
## Kappa : 0.5895
##
## Mcnemar's Test P-Value : 0.6069
##
## Sensitivity : 0.8624
## Specificity : 0.7206
## Pos Pred Value : 0.8319
## Neg Pred Value : 0.7656
## Prevalence : 0.6158
## Detection Rate : 0.5311
## Detection Prevalence : 0.6384
## Balanced Accuracy : 0.7915
##
## 'Positive' Class : 0
## rpart.rules(Model_CDT$finalModel)## .outcome
## 0.08 when Title is Master or Miss or Mrs & Pclass >= 3 & Family_size >= 5
## 0.10 when Title is Mr & Pclass < 2 & Age Group is Age.60Ov
## 0.11 when Title is Mr or Rare Title & Pclass >= 2
## 0.29 when Title is Mr & Pclass < 2 & Family_size >= 2 & Age Group is Age.1317 or Age.1839 or Age.4059 & Embarked is S
## 0.32 when Title is Mr & Pclass < 2 & Family_size < 2 & Age Group is Age.1317 or Age.1839 or Age.4059
## 0.33 when Title is Miss & Pclass >= 3 & Family_size < 5 & Age Group is Age.1317 or Age.1839 or Age.4059 & Embarked is S
## 0.53 when Title is Mrs & Pclass >= 3 & Family_size < 5 & Age Group is Age.1317 or Age.1839 or Age.4059 & Embarked is S
## 0.58 when Title is Mr & Pclass < 2 & Family_size >= 2 & Age Group is Age.1317 or Age.1839 or Age.4059 & Embarked is C
## 0.67 when Title is Rare Title & Pclass < 2
## 0.77 when Title is Master or Miss or Mrs & Pclass >= 3 & Family_size < 5 & Embarked is C or Q
## 0.78 when Title is Master or Miss or Mrs & Pclass >= 3 & Family_size < 5 & Age Group is Age.0012 or Age.60Ov & Embarked is S
## 0.94 when Title is Master or Miss or Mrs & Pclass < 34.5) Variables Importantes
Se pueden ver la importancia de las variables en ambos modelos. En ambos modelos, el título y el sexo fueron las variables más importantes para determinar si alguien sobrevivió o no.
Esta tendencia se refleja en el análisis que se realizó en la sección 3 con hombres y el título ‘Mr’ representando una tasa de supervivencia muy baja.
# Get importance
Model_DT$variable.importance## Title Sex Family_size Pclass Age Group Embarked
## 111.41503 96.41472 54.63255 31.71858 28.20113 11.29332Model_CDT$finalModel$variable.importance## Title Sex Family_size Pclass Age Group Embarked
## 114.23647 97.02466 55.44293 40.43166 29.94150 12.492174.6) Prueba Final
En esta sección, el modelo se prueba con los datos de ensayo originales con la variable dependiente oculta. Se utiliza el modelo de validación cruzada.
Al ejecutar este modelo contra los datos de ensayo, se predice que de los 418 pasajeros, 258 murieron y 160 sobrevivieron, lo que da una tasa de supervivencia del 38,28%, que está muy cerca de la tasa de supervivencia de los datos de entrenamiento del 38,38%.
set.seed(1234)
PRE_ENSAYAR=predict(Model_CDT$finalModel,newdata=total[892:1309,],type="class")
PRE_ENSAYAR## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
## 0 1 0 0 1 0 1 0 1 0 0 0 1 0 1 1 0 0 0 1
## 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
## 1 1 1 1 1 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0
## 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
## 0 0 0 1 1 0 0 0 1 1 0 0 1 1 0 0 0 0 0 1
## 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
## 0 0 0 1 1 1 1 0 0 1 1 0 0 0 1 0 0 1 0 1
## 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
## 1 0 0 0 0 0 1 0 1 1 1 0 1 0 0 0 1 0 0 0
## 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120
## 1 0 0 0 1 0 0 0 0 0 0 1 1 1 1 0 0 1 0 1
## 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140
## 1 0 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0
## 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160
## 0 1 0 0 0 0 0 0 0 0 1 0 0 1 0 0 1 0 0 1
## 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180
## 1 1 1 0 0 1 0 0 1 0 0 0 0 0 0 1 1 1 1 1
## 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200
## 0 1 1 0 1 0 1 0 0 0 0 0 1 0 1 0 1 0 0 1
## 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220
## 1 1 1 1 0 0 1 0 1 0 0 0 0 1 0 0 1 0 1 0
## 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240
## 1 0 1 0 1 1 0 1 0 0 0 1 0 0 1 0 0 0 1 1
## 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260
## 1 1 1 0 1 0 1 0 1 1 1 0 1 0 0 0 0 0 1 0
## 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280
## 0 0 1 1 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0
## 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300
## 0 1 1 1 1 0 0 0 0 0 0 1 0 1 0 0 1 0 0 0
## 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320
## 0 0 0 0 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 0
## 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340
## 0 0 0 0 1 0 1 0 0 0 1 0 0 1 0 0 0 0 0 1
## 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360
## 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 1 0 0 1
## 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380
## 0 1 1 0 1 0 0 0 1 0 0 1 0 0 1 1 0 0 0 0
## 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400
## 0 0 1 1 0 1 0 0 0 0 0 1 1 0 0 1 0 1 0 0
## 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418
## 1 0 1 0 1 0 0 1 1 1 1 1 0 0 1 0 0 1
## Levels: 0 1Ensayar_Results <- cbind(ensayo, PRE_ENSAYAR)5) Conclución
En conclusión, en esta publicación se ha creado un modelo de árbol de decisiones para clasificar si los pasajeros sobrevivieron o murieron en el Titanic. El modelo final utilizó validación cruzada para evitar un ajuste excesivo.
Cuando se probó el modelo con train_test_val, se logró una precisión del 80,79%.
Finalmente, cuando el modelo se probó utilizando los datos de la prueba, se predijo que de los 418 pasajeros del grupo de prueba 258 murieron y 160 sobrevivieron con una tasa de supervivencia del 38,28%.
Sería interesante extender este análisis en el futuro utilizando un modelo de bosque aleatorio para ver si la precisión del modelo podría mejorarse.
Gracias por leer esta publicación de dos partes. Ojalá que haya sido informativo.